Domains of Water Molecules Provide Mechanisms of Potentization in Homeopathy
of Potentization in Homeopathy
Czerlinski G1,*, Ypma T2
Key Words: water clusters, kinetics, high potency, mechano-chemical effect, radicals
Received 29 June 2009; revised 15 October; accepted 24 November. Published 21 January 2010; available online 21 January 2010.
Summary
In homeopathy, high potentization means such high dilution that there is no longer even one molecule of the original active agent per gram of the mixture. Nevertheless such high dilutions apparently remain effective. We develop a possible mechanism for homeopathic potentization to explain this phenomenon. This mechanism consists of three consecutive processes: initiation, multiplication, and amplification. Initiation is the mechano-chemical generation, by strong shaking following each dilution step, of radicals which remain in existence by mutual stabilization in simultaneously formed electronic domains. Multiplication transfers electronic excitation level structures from the original homeopathic agent to these radical-containing domains, stabilizing them further. These stabilized domains participate in the multiplication process until all the domains contain the critical information. Amplification is the generation of the same number of information-containing domains as existed prior to dilution. This amplification step can be repeated any number of times, with the original agent eventually diluted to negligible levels but the information-containing component regenerated to the same concentration in each step. In our first model we assume each domain is contained in a separate water cluster. In an alternative mechanism we consider two domains contained within one water cluster, altering the initiation process. The equations derived from these mechanisms are linked to observables (indicators) and may be used to obtain precise numbers for rate constants and concentrations from future experiments, some of which are outlined.
Article Outline
Introduction
In recent work on the action of poly-carbonyl compounds on cancer cells (Czerlinski and Ypma, 2008a) we considered extremely low concentrations of the active substance (10-12 g substance per g water), prompted by their successful use in clinical studies by Koch, 1961. Such low concentrations are not generally used in medicine, but are typical of homeopathy, which uses dilutions in which on average less (often much less) than one agent molecule is present in the administered volume. Our earlier study (loc. cit.) provides an adequate description of homeopathic action for moderate potencies (dilutions), but not for high potencies in the range of 100D (=10-100 g agent/g solution) or more. In this paper we develop possible mechanisms, involving the structure of water, that aim to explain how such high dilutions might carry and transmit the information of the original agent.
The methodology of homeopathy was introduced by Hahnemann, 1842; for details, notation and nomenclature we refer to Yasgur, 1998. The scientific literature on homeopathy is voluminous. The direction of the present study is significantly influenced by three studies that are particularly instructive of homeopathic action and are discussed below (Brizzi et al., 2000, Endler et al., 1995, Lenger et al., 2008). This selection of papers deliberately avoids work on humans, since the question of a placebo effect is difficult to avoid in human clinical trials.
Brizzi et al., 2000, used a large number of wheat seedlings and 45 x arsenic oxide As2O3 in water, corresponding to 10-45 g per g of water (Yasgur, 1998). Half of their seedlings had previously been poisoned with high concentrations of As2O3. The stem (but not the root) of the poisoned seedlings was affected by the highly diluted arsenic oxide, showing enhanced growth. They also showed that if there was no vigorous shaking after each dilution while preparing the 45 x arsenic oxide there was no effect. This highlights the requirement of intense shaking following each step of dilution in order to transmit the critical information.
Endler et al., 1995, showed that very low levels of thyroxin had an effect on the climbing of frogs from a bath immediately after metamorphosing out of their amphibian stage. When as little as 10-30 M thyroxin was added to water (corresponding to much less then one molecule per g of solution), the frogs responded by climbing out of their bath. In a particularly interesting test series, sealed ampoules with thyroxin at 10-30 M in water were inserted into the bath with frogs. This also induced the frogs to climb, apparently due to some emission from the ampoules. This suggests the presence of decaying electronic states within the homeopathic solution.
Lenger et al., 2008, showed that with high potencies (extremely low concentrations of the original agent, such as metallic silver) a light flash on a homeopathic bolus of sucrose powder produces delayed luminescence, which over a range of seconds does not decay in an exponential manner but follows a reciprocal law. Thus it seems that homeopathic dilutions contain entities which can radiate photons and have a specific photon-excitable structure. Lenger et al., 2008, mention a very low stationary luminescence, which is probably similar to the radiation coming from the sealed vials of Endler et al., 1995.
These papers suggest that strong shaking after every dilution is required to retain the activity of the original agent, photons are involved in the transmission of information, and photon absorbing structures which reemit photons in specific ways are involved. These observations underlie the mechanisms proposed below.
Since primarily water is used in homeopathic dilutions, there appears to be something in water which can retain the critical agent features after many dilutions of the agent itself. Thus we examine the structure of water and what happens to this structure upon strong shaking, both with and without a homeopathic agent. We develop two alternative mechanisms which permit the retention of critical features of the agent. We simulate these reactions under a variety of conditions by solving numerically a set of differential equations describing the model homeopathic dilution process. We use these results to develop experimental designs which could be used to test our ideas and determine specific parameter values.
Methods
(a) The initiation process
Recent data (Chaplin, 2007) suggests that water is not just H2O but consists of clusters of water molecules, denoted by (H20)n with n ranging from 2 to possibly much larger numbers. These clusters interconvert easily and quickly. Recently Smirnov et al., 2005, demonstrated the existence of giant heterophase clusters of even larger size. During the shaking that is part of the homeopathic dilution process these giant clusters may break down into smaller ones which participate in what follows.
A mechano-chemical effect takes place in water when shaken vigorously, for example in ocean surf (Domrachev et al., 1992) or during the homeopathic dilution process, which involves repeated steps of dilution followed by vigorous shaking. During such shaking, clusters with a sequence of aligned OH bonds may have synchronous movement of the aligned system which results in very rapid (1 fs) aggregation of these equal vibrational bond energies, leading to one HOH dissociating into its radicals, while the many HOH groups involved form an electronic domain. The unpaired electron in the radicals .H and .OH moves very rapidly (1 fs) between electronic isomers of individual domains of nano-sized dimension (called mesomery in organic chemistry). One element of mesomery is shown in Figure 1 (upper right), denoted “domain.”
dc1/dt = – k1 c1 (c7 + c8 + c10) + k2 (c3 + c13 + c16) + k3 (c3 + c13 + c16) – k4 c1 (c4 + c14 + c17)
dc3/dt = k1 c1 c7 – (k2 + k3) c3 + k4 c1 c4
dc4/dt = k3 c3 – k4 c1 c4 – k5 c7 c4 + k6 c5 + 2 k7 c5 – k8 (c4)2 – k20 c4
dc5/dt = k5 c7 c4 – k6 c5 – k7 c5 + ½ k8 (c4)2
dc6/dt = k10 c7 c8 – k9 c6
dc7/dt = – k10 c7 c8 + k9 c6 – k11 c7 c9 + k12 c10 – k16 c7 – k1 c1 c7 + k2 c3 + k6 c5 – k5 c7 c4
dc8/dt = – k10 c7 c8 + k9 c6 – k13 c8 – k1 c1 c8 + k2 c13 + k6 c15 – k5 c8 c14
dc9/dt = – k11 c7 c9 + k12 c10 + k19 c21 – k18 c19 c9
dc10/dt = k11 c7 c9 – k12 c10 – k14 c10 – k1 c1 c10 + k2 c16 + k6 c18 – k5 c10 c17
dc11/dt = ½ k15 (c20)2 + k15 c19 c21
dc12/dt = ½ k17 (c19)2
dc13/dt = k1 c1 c8 – k2 c13 – k3 c13 + k4 c1 c14
dc14/dt = k3 c13 – k4 c1 c14 – k5 c8 c14 + k6 c15 + 2 k7 c15 – k8 (c14)2 – k20 c14
dc15/dt = k5 c8 c14 – k6 c15 – k7 c15 + ½ k8 (c14)2
dc16/dt = k1 c1 c10 – k2 c16 – k3 c16 + k4 c1 c17
dc17/dt = k3 c16 – k4 c1 c17 – k5 c10 c17 + k6 c18 + 2 k7 c18 – k8 (c17)2 – k20 c17
dc18/dt = k5 c10 c17 – k6 c18 – k7 c18 + ½ k8 (c17)2
dc19/dt = k20 c4 + k19 c21 – k18 c19 c9 – k15 c19 c21 – k17 (c19)2 + k16 c7
dc20/dt = k20 c14 – k15 (c20)2 + k13 c8
dc21/dt = k20 c17 – k15 c19 c21 – k19 c21 + k18 c19 c9 + k14 c10
c60 = c6 + c11 + c12 + c5 + c15 + c18 + ½ (c7 + c8 + c10 + c3 + c4 + c13 + c14 + c16 + c17 + c19 + c20 + c21)
c10 = c1 + c3 + c13 + c16
Table 1: Differential Equations Defining the Mechanism of Figure 1
The proposed mechanism has two components; one in which the shaking of water produces radicals, and another in which a transfer of characteristics of the original homeopathic agent to the nano-domains occurs. Since this information can apparently also be transferred by photons, we surmise that the characteristics are the electronic excitation level structures of the original agent.
Figure 1 shows such a mechanism (Model 1), with the radical formation shown in part A and an information copying section in part B. Here we discuss part A; in section (b) below we discuss part B. The subsequent information amplification process which occurs in repeated dilutions with shaking is discussed in section (c).
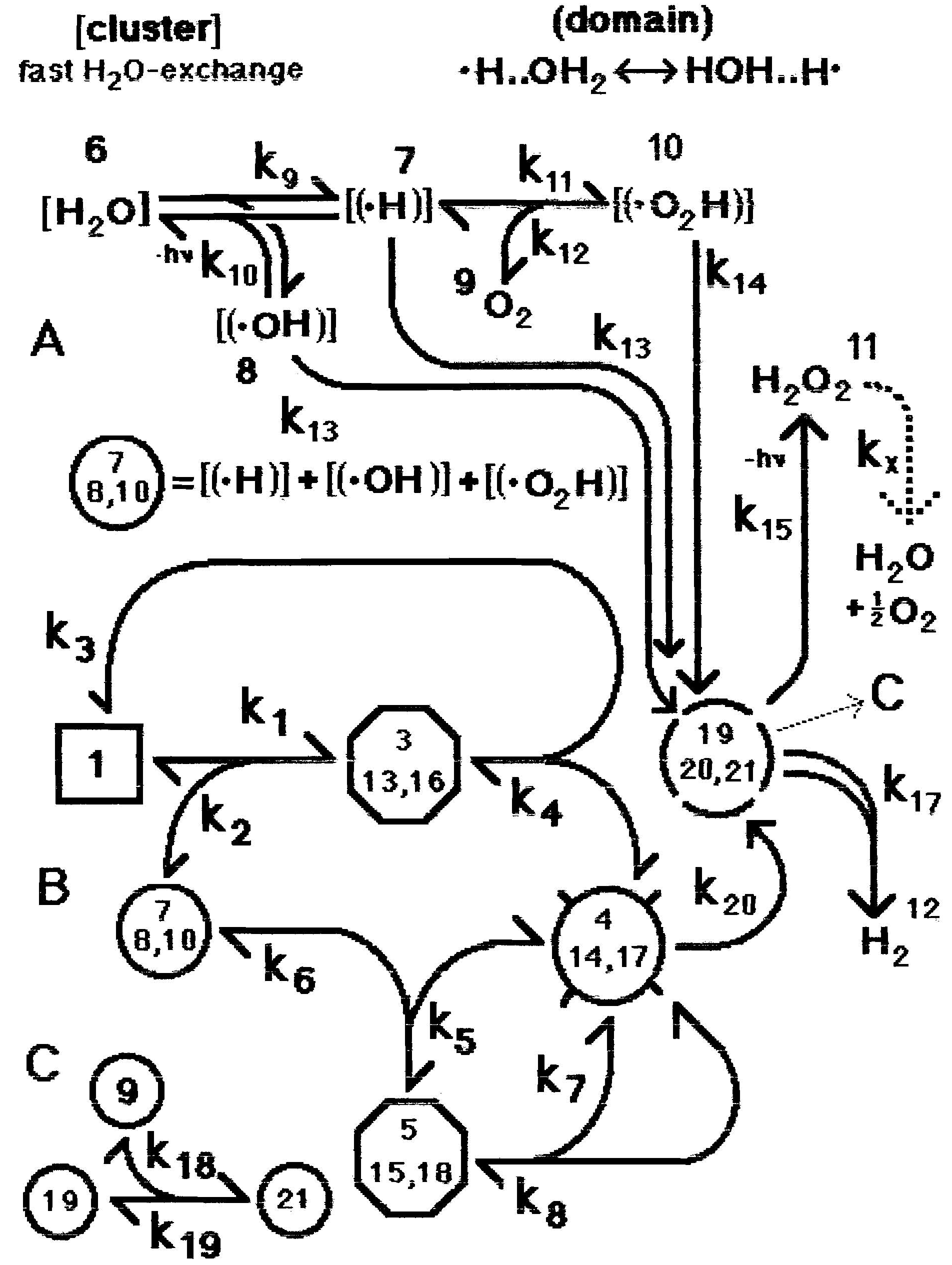
Figure 1: Full mechanism of homeopathic amplification (Model 1). Part (A) shows the formation of sub-clusters with one H2O molecule being split into radicals stabilized in domains. Fast reacting free radicals only appear after breakdown of the domains. These free radicals are numbered 19, 20 and 21 for .H, .OH and .O2H respectively. In (B) component 1 is the original effective agent, while component 2 is a cluster with all the radicals involved in the copying process of the properties of component 1. Component 4 carries the crucial information of component 1 in the form of photo-excitation states over a wide spectrum of photon energies. This spectrum is characteristic of the agent and is imprinted from component 1. Amplification takes place when component 1 is diluted followed by strong shaking but component 4 after copying reaches the same stationary concentration regardless of the number of dilution steps. Figure 1C describes a reaction between free radicals involving dissolved O2.
In Figure 1A there are two paths between component 6 (the initial water cluster) and the pair 7 and 8 (the radicals in new domains), with microscopic reversibility assumed for both. The corresponding back rate constant k9r (not shown) is very small compared to the parallel moving reverse photo-chemical k10. The counter-flowing photo-chemical rate constant k10r is solely determined by the number of photons of wave length around 175 nm absorbed by H2O to produce radicals. Since this number of photons is negligibly small on the surface of the earth, the composite k10r is significantly less than k9. Since this back reaction with k10r does not include domain formation, compounds 7 and 8 are not formed from this reaction and the photo-chemical radicals produced are short-lived. In short, since the conversion from component 6 to 7 involves k9 (a mechano-chemical conversion) while that from 7 to 6 involves k10 (a reverse photo-chemical conversion) and k10 (c7 + c8) << k9, essentially all of convertible component 6 is converted to 7 and 8.
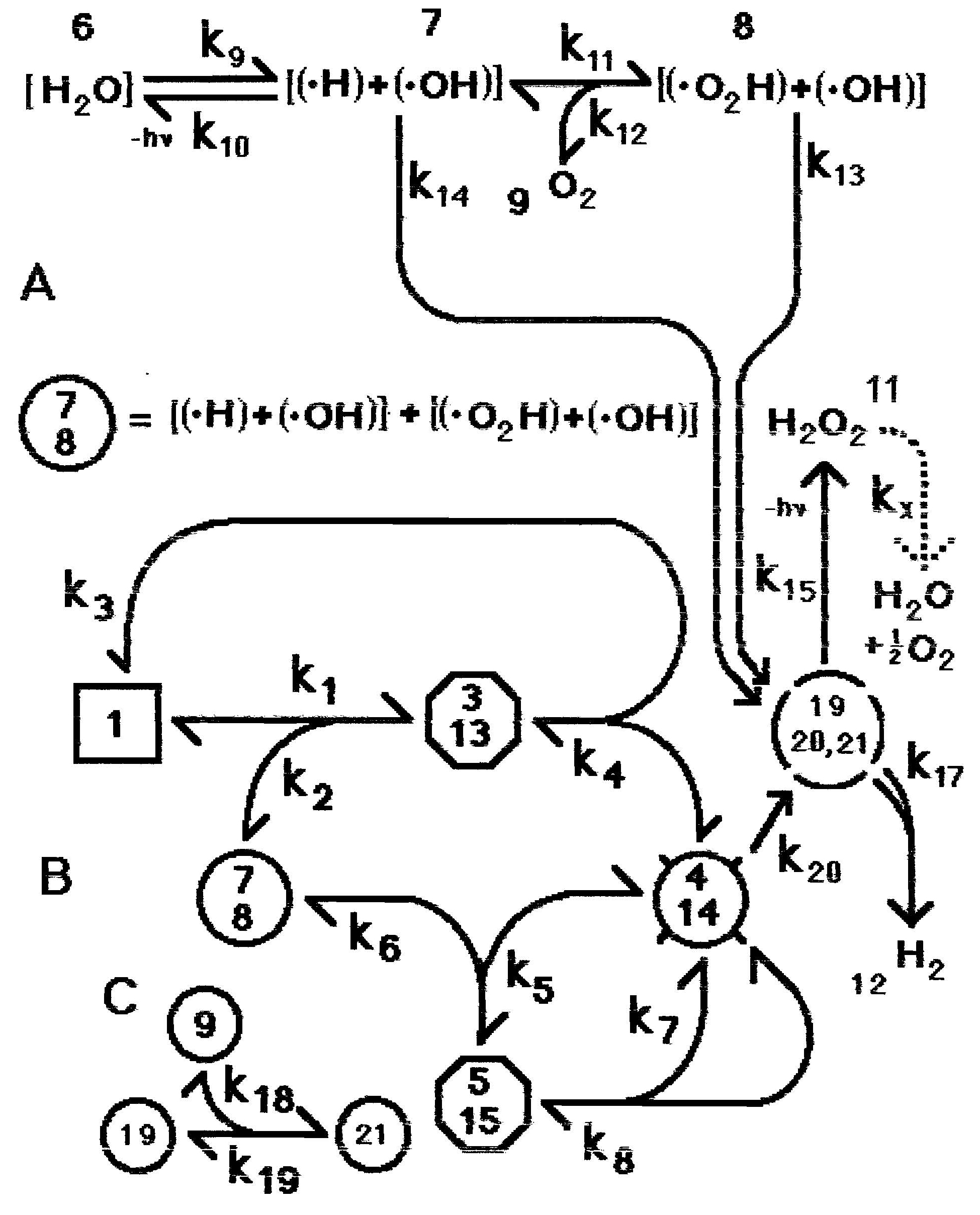
Figure 2: Alternative mechanism of homeopathic amplification (Model 2), now involving the initial formation of two radical-containing domains within each cluster. Otherwise as in Figure 1.
Molecular oxygen is not usually excluded from an aqueous system. When dissolved molecular oxygen (component 9) is present the second step in Figure 1A takes place, producing component 10. The equilibrium concentration of component 10 depends on the ratio c9 / (k12/k11): the larger this ratio, the more component 10 is produced (assuming c9 > c7). In distilled water components 7, 8 and 10 likely convert to H2O2 in at most a few hours, the average life time of H2O2 in the atmosphere (Selivanovsky et al., 2008). Using c8 = 10-6 M and setting the length of time for this conversion to be 1/k13 = 105 s (on the high side) gives k13 = 10-5 s-1. We set 10 k16 = k14 = k13.
As indicated in Figure 1A the generation of H2O2 is associated with the release of photons. There may be a reverse k15r, equivalent to a photo-chemical splitting of H2O2 into its radicals. We assume that the energy needed for splitting is high while the number of photons is low, thus this effect is negligible.
To obtain more precise parameter values, experiments must be conducted. When a solution of radicals is mixed with a solution of dissolved oxygen, one should be able to observe the concentration changes of the reactants using fluorescent indicators. Alternatively, one could pre-mix component 6 with varying amounts of component 9 (oxygen), then initiate the mechano-chemical effect and observe the kinetics of radical generation over a range of O2 concentrations. Extrapolation to zero oxygen concentration would then provide kinetic data for the generation of components 7 and 8.
( b ) The information copying process.
Figure 1B describes the mechanistic details of the information transfer that takes place in the dilution process when combined with vigorous shaking. Classical fluorescence reveals that excitation energy transfer can take place over distances of up to 5 nm (Foerster, 1951). If the emitting and reabsorbing molecules have overlapping emission and absorption spectra and their distance is 5 nm or less, the transferred energy can be used for a photo-chemical change, such as the isomerization investigated by Gole and Michels, 1995. Since there is no photo-excitation energy available we postulate a different effect: an excitation energy level transfer from agent molecules to domains within 5 nm. We assume that the free electron in the domain can easily accept the excitation energy levels of the agent.
In Figure 1B component 1 is the small molecule with the homeopathic action of interest. All other components (except for the terminal H2 and H2O2, as well as the short-lived components 19, 20 and 21) are water clusters containing domains. In complex 3 the excitation level structure is transferred from component 1 to component 7 (or 8 or 10, see below). Complex 3 then dissociates into component 1 and a new component 4 which contains the transferred information. Component 4 contains the ‘memory component’ referred to by some homeopaths. Since component 4 contains the crucial information of component 1, it can act like component 1, forming the binary complex 5, which after the information (i.e., the excitation level structure of the original agent) transfer dissociates into two components 4. Figure 1C accounts for the presence of O2.
We introduce the terms
c*3 = c3 + c13 + c16,
c*4 = c4 + c14 + c17,
c*5 = c5 + c15 + c18, and
c*7 = c7 + c8 + c10.
as the radical concentrations produced in the steps with k1, k3, k5 and k9 respectively. In these relations c3, c4, c5 and c7 all contain the hydrogen radical; c8, c13, c14 and c15 all contain the hydroxyl radical, and c10, c16, c17 and c18 all contain the radical . O2H.
Since k4 and k8 are extremely small, c4* is quickly formed without reverse flow, and then stays essentially constant as the sum c4SS + c14SS + c17SS (where the subscript SS refers to a stationary state) due to the relatively slow conversion of components 4, 14 and 17 to component 11 (H2O2) via the short-lived free radicals. Since component 6 splits into two radicals within domains and any subsequent reactions proceed relatively rapidly, the sum of these initial products is given by c*7 which is then consumed via c*3 and c*5 to give approximately c4* = 2 c60.
As mentioned earlier, Endler et al., 2005, reported effects on the climbing rate of frogs when using a thyroxin solution in sealed ampoules. That solution was highly diluted in several steps, with vigorous shaking, so single-electron domains in clusters of water were present as described above. We postulate that the radiation from the sealed vials of Endler et al., 2005, and also the low-level long-term luminescence of Lenger et al., 2008, are associated with the recombination of radicals. The lifetime of the radiation from the recombination of two radicals in the stabilized domains is much longer than the few hours observed for the recombination processes controlled by k13, k14 and k16. The photons required to explain the sealed ampoule effects described by Endler et al., 2005, might be formed after decay of component 14 to 20 (k20) and their subsequent collapse to give H2O2. This photon release is indicated in Figure 1B by ‘–hν’ next to the arrow with k15. Since the information copying process stabilizes the domain, we require k20 << k13. Since these photons mimic the presence of the agent, they must have been contained in the electronic precursors in the domains, which means that an effective information transfer must have taken place in component 3 (plus 13 and 16). Popp, 1998, estimates 10-9 s as approximate life time of the information carrying component. We therefore estimate 1/k20 = 10-10 s. It appears that the long-lived domains do not behave like ordinary molecules, but more like biophoton receivers and emitters. A good overview of the latter is provided by Popp et al., 1992.
( c ) The information amplification process.
Initially the value of c*4 is zero, but c*4 > 0 for all subsequent phases of dilution and shaking. Let k count the dilution phases, so k = 0 defines the initial phase, and define rd as the dilution ratio (typically rd = 0.1, 0.01, or 0.001). While each dilution step starts with the same value of c60, the successive initial values of c1 , denoted (c10)k , satisfy (c10)k = rdk (c10)0. Similarly after each dilution (c4SS*)k = rd (c4SS*)k-1, but following the dilution and shaking the initial c60 converts to c4*, with the result that subsequently (c4SS*)k = (c4SS*)k-1. Thus the concentration of component 1 becomes progressively smaller, but the stationary concentrations of components 4, 14 and 17 only change within a limited range irrespective of the number of dilution steps. An example is shown in Figure 4 for k = 1 and rd = 0.01.
The upper values of the diffusion limited bimolecular reaction rate constants in water are largely determined by the size of the molecules involved. The values of k1 and k4 are primarily determined by component 1, which is usually a relatively small molecule. However, the bimolecular rate constants k5 and k8 both involve water clusters, which diffuse slower than component 1. This means that the (limiting) diffusion controlled bimolecular rate constants are smaller than those for small molecules and appropriate values need to be computed. Equation (1) of Czerlinski and Ypma, 2008b, was used to estimate the constants given in Tables 2 and 4.
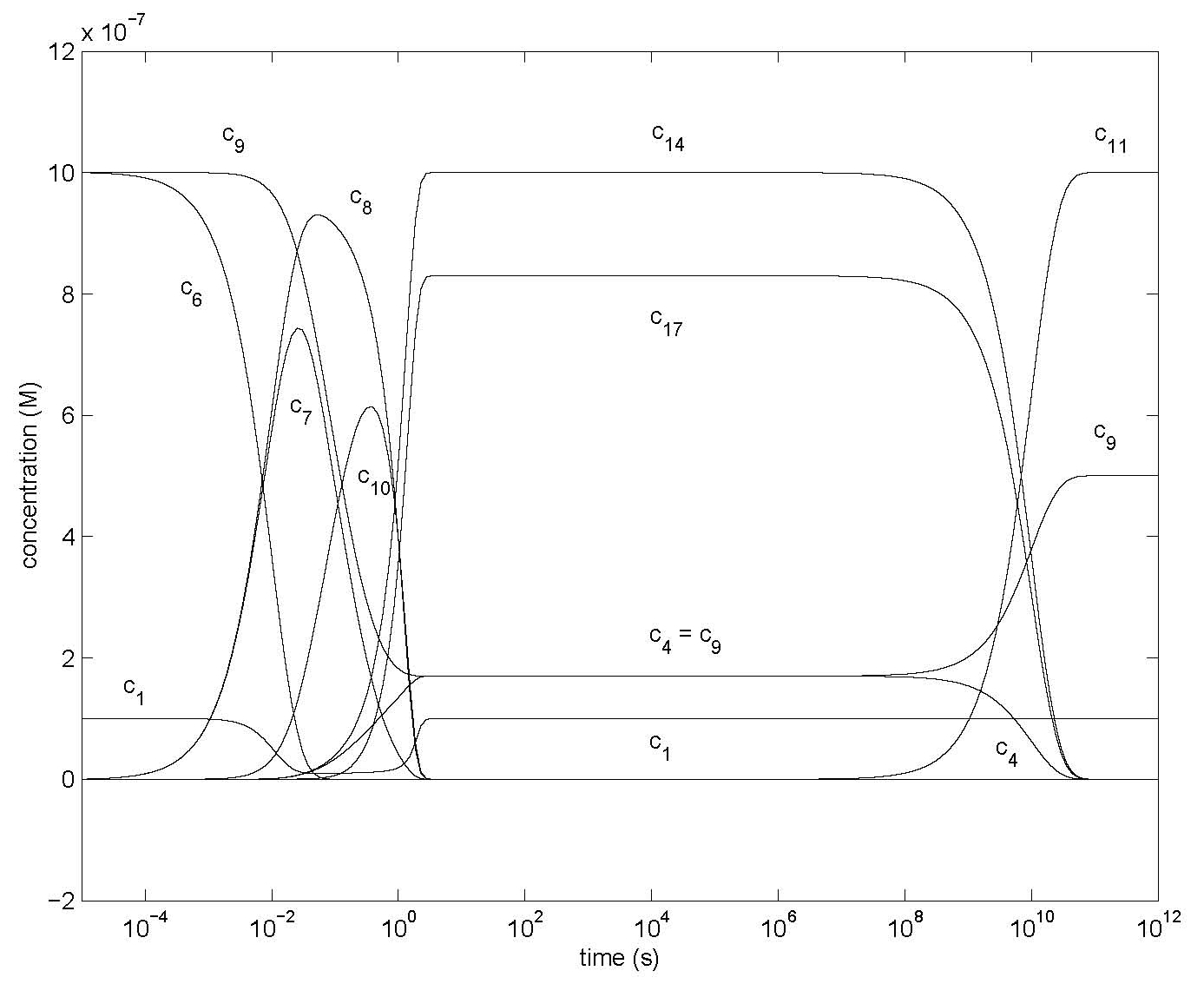
Figure 3: Changes of concentrations of most species of Model 1 in Figure 1 using the differential equations of Table 1, showing specifically c1, c4, c6, c7, c8, c9, c10, c11, c14, c17 with all ci0 = 0 except c10 = 10-7 M, c60 = c90 = 10-6 M. Other parameter values are in Table 2.
| DESCRIPTION |
SYMBOL |
VALUE |
UNITS |
NOTE |
||||
| Initial concentration of component 1 |
c10 |
0, 10-7 |
M |
1 |
||||
| Initial concentration of component 6 |
c60 |
10-6 |
M |
2 |
||||
| Initial concentration of component 9 |
c90 |
0, 10-6 |
M |
3 |
||||
| Other initial concentrations |
ci0 |
0 |
M |
|||||
| Compounds with H-radical |
7, 3, 4, 5, 19 |
|||||||
| Compounds with OH-radical |
8, 13, 14, 15, 20 |
|||||||
| Compounds with O2H-radical |
10, 16, 17, 18, 21 |
|||||||
| Time period of intense shaking |
tS |
10 |
s |
2 |
||||
| Rate constant for multiplication |
k1 |
108 |
M-1 s-1 |
4 |
||||
| Rate constant for multiplication |
k2 |
10 |
s-1 |
2 |
||||
| Rate constant for multiplication |
k3 |
10 |
s-1 |
2 |
||||
| Rate constant for multiplication |
k4 |
10-10 |
M-1 s-1 |
2 |
||||
| Rate constant for multiplication |
k5 |
106 |
M-1 s-1 |
= k1/100 |
||||
| Rate constant for multiplication |
k6 |
10-1 |
s-1 |
= k2/100 |
||||
| Rate constant for multiplication |
k7 |
10 |
s-1 | = k3 |
||||
| Rate constant for multiplication |
k8 |
10-10 |
M-1 s-1 |
= k4 |
||||
| Mechano-chemical rate constant |
k9 |
100 |
s-1 |
5 |
||||
| Reverse mechano-chem. rate constant |
k9r |
10-9 |
M-1 s-1 |
2 |
||||
| (reverse) photo-chem. rate constant |
k10 |
10-2 |
M-1 s-1 |
2 |
||||
| (forward) photo-chem. rate constant |
k10r |
10-9 |
s-1 |
2 |
||||
| Oxygen consumption rate constant |
k11 |
107 |
M-1 s-1 |
= k1/10 |
||||
| Oxygen dissociation rate constant |
k12 |
10-1 |
s-1 |
2 |
||||
| Slow radical recombination rate constant |
k13 |
10-5 |
s-1 |
2 |
||||
| Slow radical recombination rate constant |
k14 |
10-5 |
s-1 |
= k13 |
||||
| Slow radical recombination rate constant |
k15 |
106 |
M-1 s-1 |
= k1/100 |
||||
| Slow radical recombination rate constant |
k16 |
10-6 |
s-1 |
= k13/10 |
||||
| Slow radical recombination rate constant |
k17 |
104 |
M-1 s-1 |
= k15/100 |
||||
| Final oxygen binding rate constant |
k18 |
107 |
M-1 s-1 |
= k11 |
||||
| Final oxygen regen. rate constant |
k19 |
10-1 |
s-1 |
= k12 |
||||
| Slow isomerize domain to random |
k20 |
10-10 |
s-1 |
= k9r/10 |
||||
| Component 7 consumption constant |
t1 |
0.02 |
s |
= (k2 + k3)/ (c60 k1 k3) |
||||
| Radical formation time constant |
t9 |
0.1 |
s |
= 1/k9 |
||||
| Decay time constant, Figure 1A |
t13 |
105 |
s |
= 1/k13 |
||||
| Decay time constant, Figure 1B |
t20 |
1010 |
s |
= 1/k20 |
||||
3) Any value within a wide range could be used; we set c90 = c60 for high conversion of the produced c7.
4) Eq. (1) provides upper limit
5) Changes to 0 at time tS = 10s
Table 2: Parameters in
Figure 1.( d ) Model 2: An alternative mechanism.
The slowest step in the overall reaction involving k9 is probably the dissociation into the two daughter clusters. If the generated electrons are sufficiently uncoupled in the newly formed domains this dissociation does not need to occur. This produces the alternative mechanism of Figure 2. For simplicity we assume that in complexes 3 and 5 information is transferred from compound 1 to both domains within compound 2. Otherwise, k9 here results from the same processes described for k9 in Figure 1, while in Figure 2 k10 becomes a monomolecular rate constant for which a value could be experimentally determined from the slow disappearance of radicals when oxygen is excluded. The distinction between these two alternative mechanisms is the first step. We assume that domains in clusters of type {(.H) + H2O2} are very short-lived.
The model of Figure 2 is described by the differential equations in Table 3. We simulate this system using the constants in Table 4. Figure 5 shows the computed results.
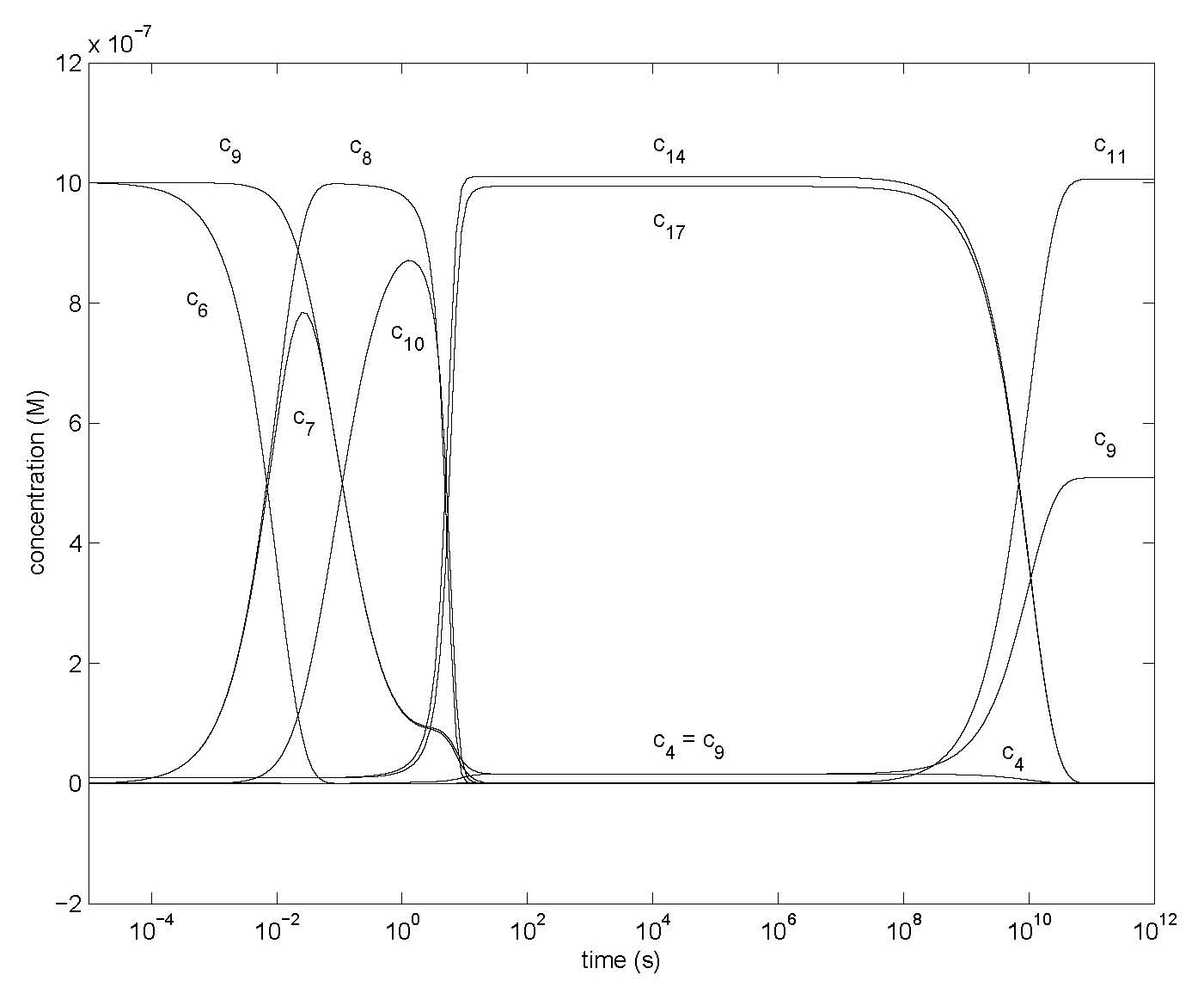
Figure 4: Changes of concentrations of most species of Model 1 after first amplification step with rd = 0.01 for Model 1 (Figure 1) with the differential equations of Table 1, showing concentrations c1, c4, c6, c7, c8, c9, c10, c11, c14, c17 with all ci0 = 0 except c10 = 10-9 M, c140 = c170 = 10-8 M, c60 = c90 = 10-6 M (essentially c40 = 0 with oxygen present). Other parameter values are in Table 2.
dc1/dt = – k1 c1 (c7 + c8) + (k2 + k3) (c3 + c13) – k4 c1 (c4 + c14)
dc3/dt = k1 c1 c7 – (k2 + k3) c3 + k4 c1 c4
dc4/dt = k3 c3 – k4 c1 c4 – k5 c7 c4 + k6 c5 + 2 k7 c5 – k8 c42 – k20 c4
dc5/dt = k5 c7 c4 – k6 c5 – k7 c5 + ½ k8 c4 2
dc6/dt = k10 c7 – k9 c6
dc7/dt = k9 c6 – k10 c7 – k11 c7 c9 + k12 c8 – k1 c1 c7 + k2 c3 + k6 c5 – k5 c7 c4 – k13 c7
dc8/dt = k11 c7 c9 – k12 c8 – k1 c1 c8 + k2 c13 + k6 c15 – k5 c8 c14 – k14 c8
dc9/dt = – k11 c7 c9 + k12 c8 – k18 c19 c9 + k19 c21
dc10/dt = 0 = c10
dc11/dt = ½ k15 c202 + k15 c19 c21
dc12/dt = ½ k17 c192
dc13/dt = k1 c1 c8 – k2 c13 – k3 c13 + k4 c1 c14
dc14/dt = k3 c13 – k4 c1 c14 – k5 c8 c14 + k6 c15 + 2 k7 c15 – k8 c14 2 – k20 c14
dc15/dt = k5 c8 c14 – k6 c15 – k7 c15 + ½ k8 c14 2
dc19/dt = k20 c4 – k18 c19 c9 + k19 c21 + k13 c7 – k17 c192 – k15 c19 c21
dc20/dt = k20 c4 + k20 c14 + k13 c7 + k14 c8 – k15 c202
dc21/dt = k20 c14 + k18 c19 c9 + k14 c8 – k19 c21– k15 c19 c21
c60 = c6 + c7 + c8 + c3 + c4 + 2 c5 + c13 + c14 + 2 c15 + ½ (c19 + c20 + c21)
c10 = c1 + c3 + c13
Table 3: Differential Equations Defining the Mechanism of Figure 2.
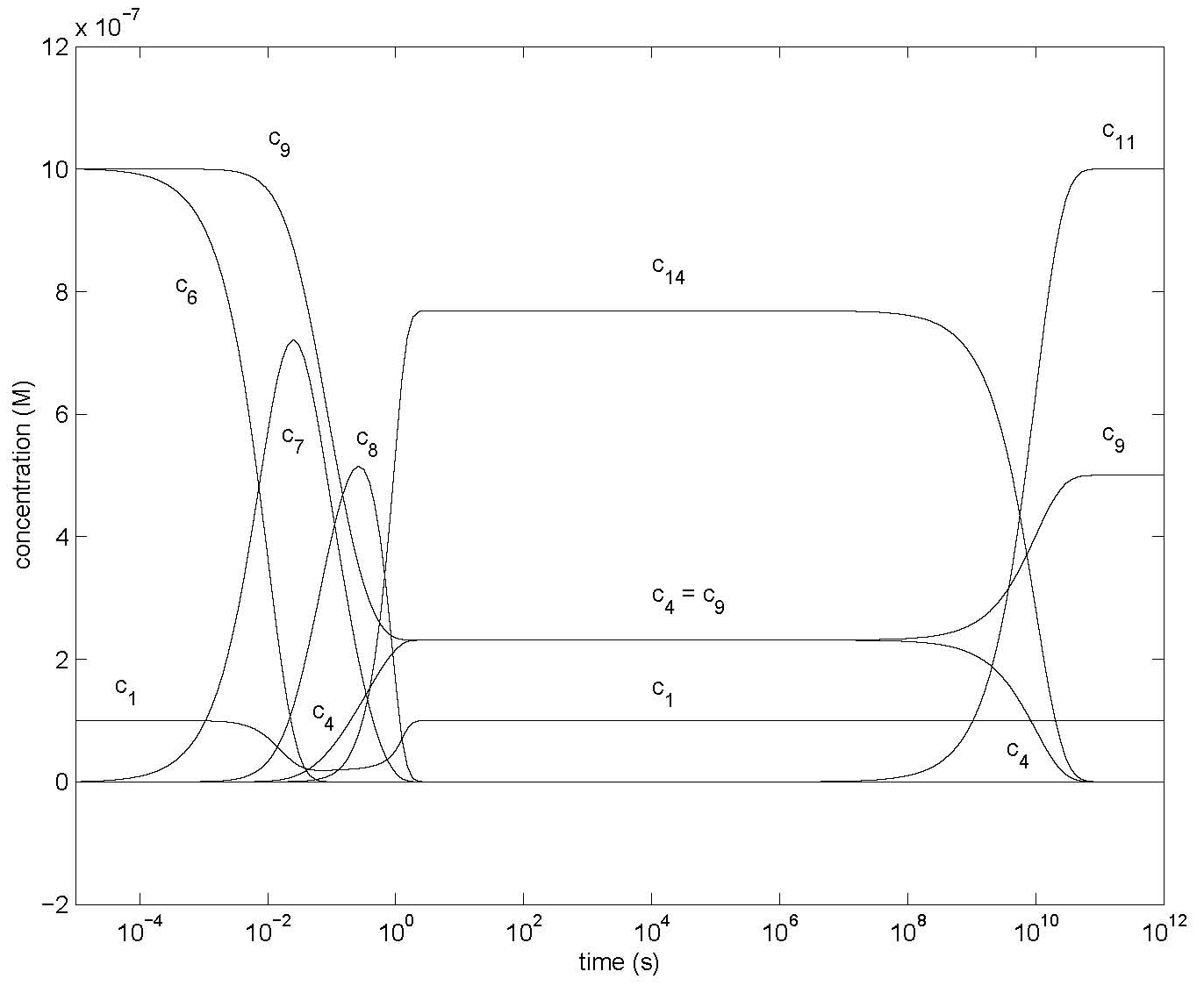
Figure 5: Changes of concentrations of most species of Model 2 (Figure 2) using the differential equations of Table 3, showing concentrations c1, c4, c6, c7, c8, c9, c11, c14 after dilution (and shaking) with all c10 = 0 except c10 = 10-9 M, c60 = c90 = 10-6 M. Other parameter values are in Table 4.
| DESCRIPTION | SYMBOL | VALUE | UNITS | NOTES | |
| Initial concentrations | ci | same as in Table 2 | |||
| Compounds with OH- and H-radical | 7, 3, 4, 5 | 1 | |||
| Compounds with OH- and O2H-radical | 8, 13, 14, 15 | 1 | |||
| Rate constant for multiplication | k1 | 108 | M-1 s-1 | 2 | |
| Rate constant for multiplication | k2 | 10 | s-1 | 2 | |
| Rate constant for multiplication | k3 | 10 | s-1 | 2 | |
| Rate constant for multiplication | k4 | 10-10 | M-1 s-1 | 2 | |
| Rate constant for multiplication | k5 | 106 | M-1 s-1 | 2 | |
| Rate constant for multiplication | k6 | 10-1 | s-1 | 2 | |
| Rate constant for multiplication | k7 | 10 | s-1 | 2 | |
| Rate constant for multiplication | k8 | 10-10 | M-1 s-1 | 2 | |
| Mechano-chemical rate constant | k9 | 100 | s-1 | 4 | |
| Reverse mechano-chem. rate const. | k9r | 10-9 | s-1 | 3 | |
| (reverse) photo-chem. rate const. | k10 | 10-2 | s-1 | 2 | |
| (forward) photo-chem. rate const. | k10r | 10-9 | s-1 | 2 | |
| Oxygen consumption rate constant | k11 | 107 | M-1 s-1 | 2 | |
| Oxygen dissociation rate constant | k12 | 10-1 | s-1 | 2 | |
| Slow radical recombination rate const. | k13 | 10-5 | s-1 | 2 | |
| Slow radical recombination rate const. | k14 | 10-5 | s-1 | 2 | |
| Slow radical recombination rate const. | k15 | 106 | M-1 s-1 | 2 | |
| Slow radical recombination rate const. | k17 | 104 | M-1 s-1 | 2 | |
| Final oxygen binding rate constant | k18 | 107 | M-1 s-1 | 2 | |
| Final oxygen regen. rate constant | k19 | 10-1 | s-1 | 2 | |
| Slow isomerize domain to random | k20 | 10-10 |
s-1 |
2 |
|
3) Any value within a wide range could be used; we set c90 = c60 for high conversion of the produced c7.
4) Eq. (1) provides upper limit
5) Changes to 0 at time tS = 10s
Table 4: Parameters in
Figure 2.
Results and Discussion
(a) Testing of the first model.
The concentration changes involving components 6, 7 and 8 with c60 > 0 and c70 = c80 = c90 = 0 M obtained by our numerical simulations of the mechanism of Figure 1A are not shown, but gave the expected behavior with c11 and c12 both growing at the end to ½ c60. The appearance of radicals (such as c7 and c8) might be observed by using the fast optical methods developed by Zafiriou et al, 1990, who used NO and aliphatic NO derivatives to observe the appearance of radicals in sea water. In the presence of oxygen, given by c60, c90 > 0 and all other initial concentrations zero, the appearance of radicals may similarly be observed. A full evaluation may require increasing the oxygen concentration stepwise over the dependent range.
Figure 3 shows the results for c10, c60, c90 > 0 and all other initial concentrations zero. In this case the addition of NO or its derivatives would not distinguish between the various compounds; special reactants (such as derivatives of NO) to detect the presence of component 4 have to be developed. Domrachev et al, 1992, used luminol to detect low levels of H2O2. When only component 4 is present an increase in the H2O2 concentration corresponds to a decrease in c4. Alternatively, the photo-chemical properties of component 4 may be used to quantify its concentration. The transient decrease in c1 is due to the formation of c*3; a much shorter delayed transient increase of c*5 appears in the same area. To enhance visibility of the rising curves neither c*3 or c*5 is shown. The sum c*4 of the flat (stationary state) portions of c4, c14 and c17 is 2 x 10-6 M = 2 c60 as expected.
Figure 4 shows the first step of amplification. The low initial concentrations (before shaking the mixture) of components 1 and 4 are not visible. The increase in concentrations of 4 and 14 forms a sharp corner upon reaching its maximum, more so in Figure 4 than in 3 where a substantial amount of component 1 is present and reduces this effect. Compounds 3* and 5* might be regarded as enzyme-substrate complexes. But since the product 4* of 5* is also its enzyme we have auto-catalysis by this product. The sum c*4 of the flat (stationary state) portions of c4, c14 and c17 is again 2 x 10-6 M = 2 c60.
(b) Testing of the second model.
Figure 5 (Model 2) is comparable to Figure 3 (Model 1). The key difference for experimental observation lies in the mechano-chemical conversion of a water molecule into its radicals. Experiments have to be designed to ensure that the difference between the two models shows up. This difference is largest when approximately c60 = 2 k9/k10, otherwise there is little concentration dependence in the kinetics (Czerlinski, 1966). The sum c*4 of the flat (stationary state) portions of c4 and c14 in Figure 5 is now 10-6 M = c60 (as distinct from Figure 3).
(c) Homeopathic dilution in solid media.
Two of the three homeopathic references discussed in the introduction used liquid media, while Lenger at al, 2008, used a solid medium. Solid media are generally used whenever insoluble substances are used as homeopathic agents (Yasgur, 1998). Although lactose is conventionally used as the solid medium, Lenger at al, 2008, used sucrose. Vigorous movement of an aqueous system leads to the mechano-chemical effect in water, and the grinding of sugar crystals in an agate mortar has a similar effect. When breaking a crystal, the pestle is hitting a smaller crystal beneath, initiating synchronous vibrations along lined-up bonds in the crystal. As in a water cluster, these lined-up vibrations stabilize into a domain with radicals generated within 1 fs. The domain and radical again stabilize each other. Since we have a solid phase, many of the reactions of the generated domains are much slower than in the liquid phase, but otherwise the mechano-chemical effect in solids is very similar to the one in liquids described above. Mechano-chemical effects in organic crystals with initial formation of radicals have been repeatedly described (Aleksandrov et al., 1999).
(d) Photonic effects and their measurement
The rate constant k20 is associated with the termination of the existence of the information storage compounds. No ‘hν’ is shown near the arrow with k20 in Figure 1, implying that any decrease in energy of the domain due to its collapse is dissipated. No increase in temperature will be detected, since the concentration is small and the process is slow. If photons are emitted, one should be able to measure this by highly sensitive photodetectors, an increase in sampling time and a wider spectral observation range than used by Lenger et al., 2008. Spectral information on the electronic structure of the domains (such as compound 4) can be obtained by flash experiments similar to those of Lenger et al., 2008. Although the equivalent of k20 is also present in Figure 1A, it is there much smaller and refers to rate constants k13 and k14 which are of less importance.
Conclusion
We have developed a mechanism for homeopathic potentization consisting of three processes: initiation, multiplication (copying), and amplification. Initiation is the mechano-chemical generation of radicals contained in electronic domains, with mutual stabilization. Multiplication transfers electronic excitation level structures from the homeopathic agent to these radical-containing domains, stabilizing them further. These domains participate in the multiplication process until all domains are consumed. Amplification is the dilution of a prior solution followed by strong shaking which repeats the initiation and multiplication process. This amplification can be repeated any number of times, with the original agent diluted to negligible levels but the information containing component regenerated to the same concentration in each step.
Several experiments have been suggested. Other questions should also be addressed. For example, the rate constants k9r, k10r, k4, k8 could be much smaller than presented in Tables 2 and 4. If so, irreversible thermodynamics may have to be taken into account. If the electron in the domain moves statistically this could produce domains with the electron moving like a dipole, initiating similar behavior in other domains by resonance.
Acknowledgment
The authors thank Jana Shiloh and Karin Lenger for introducing them to the questions studied here and providing useful references.
References
Aleksandrov, AI; Aleksandrov, IA; Prokofev, AI; Bubnov, NN, (1999). Pulse mechanochemnistry of organoelement compounds, Russian Chemical Bulletin 48: 1599 – 1614.
Brizzi, M; Nani, D; Peruzzi, M; Betti, L, (2000). Statistical analysis of the effect of high dilutions of arsenic in a large dataset from a wheat germination model, Br. Homeop. J. 89: 63 – 67. Based in part on Betti, L; Brizzi, M; Nani, D; Peruzzi, M, (1997). Effect of high dilutions of arsenicum album on wheat seedlings poisoned with the same substance, Br. Homeop. J. 86: 86 –89.
Chaplin, M, (2007). The memory of water: an overview. Homeopathy 96: 143 – 150.
Chaplin, M, (2008). Reply to comment on `The memory of water: an overview’, Homeopathy 97: 43 – 44.
Cowan, ML; Bruner, BD; Huse, N; Dwyer, JR; Chugh, B; Nibbering, ETG; Elsaesser, T; Miller, RJD, (2005). Ultrafast memory loss and energy redistribution in the hydrogen bond network of liquid H2O, Nature 434: 199 – 202.
Czerlinski, GH, (1966). Chemical Relaxation, Marcel Dekker: New York.
Czerlinski, GH; Ypma, TJ, (2008a). Single molecule action in cancer cells, J. Bionanoscience 2: 9 – 18.
Czerlinski, GH; Ypma, TJ, (2008b). Dimensional effects on single molecule kinetics in submicron vacuoles, J. Bionanoscience 2: 19 – 28.
Domrachev, GA; Rodygin, YuL; Selivanovski, DA, (1992). The role of sound and of liquid water as a dynamically unstable polymeric system in mechano-chemically activated oxygen-generating processes under terrestrial conditions, Russian J. Phys. Chem. 66: 457 – 460.
Endler, PC; Pongratz, W; Smith, CW; Schulte, J; 1995, Non-molecular information transfer from thyroxine to frogs with regard to homeopathic toxicology, Vet. Human Toxicol. 37: 259 – 260.
Foerster, Th, (1951). Fluoreszenz Organischer Verbindungen, Vandenhoeck and Ruprecht, Goettingen.
Gole, JL, Michaels, HH, 1995, High specific enthalpies from the photo-chemically induced isomerization: BOH <– –> HBO, J. Chem. Phys. 103: 7844 – 7850.
Hahnemann, S, (1842). Organon of Medicine, translated into English by Kuenzli, J; Naude, A; Pendleton, P, (1982). JP Tarcher Inc., Los Angeles, CA.
Koch, WF, (1961). The Survival Factor in Neoplastic and Viral Diseases, The Vanderkloot Press: Detroit, MI.
Lenger, K; Bajpai, RP; Drexel, M, (2008). Delayed luminescence of high homeopathic potencies on sugar globuli, Homeopathy 97: 134–140.
Matlab 7.0, (2004). The Mathworks, 24 Prime Park Way: Natick, MA.
Popp, F-A, (1992). Some essential questions of biophoton research and probable answers, in Popp, F-A; Li, KH; Gu, Q; Eds, Recent Advances in biophoton research and its applications, World Scientific, Singapore: 1 – 45.
Popp, F-A , (1998). Hypothesis of modes of action of homeopathy: theoretical background and the experimental situation, in Ernst, E, and Hahn, EG, Homeopathy, a critical appraisal, Butterworth-Heinemann, London: 145 – 152.
Shampine, LF; Reichelt, MW, (1997). The Matlab ODE suite, SIAM J. Sci. Comput. 18: 1 – 22.
Smirnov, AN; Lapshin, VB; Balyshev, AV; Leb
Yasgur, J, (1998). Homeopathic Dictionary and Holistic Health Reference. 4th ed., Van Hoy Publishers, Greenville: 193-198.
Zafiriou, OC; Blough, NV; Micinski, E; Dister, B; Kieber, D; Moffett, J, (1990). Molecular probe systems for reactive transients in natural waters, Marine Chemistry 30: 45 – 70.
Websites
Selivanovsky, DA, Domrachev, GA, Didenkulov, IN, Stunzhas, PA, 2008, Hydrogen peroxide is the source of oxygen in the atmosphere (version of Nov. 29, 2008) http://www.scienceandfuture.sgm.ru/2004/files/eng/086_01.pdf
Discussion With Reviewers
Anonymous Reviewer: Could the mechano-chemical effects of agitation involve other entities, such as, container surfaces, cavitation of micro-, nano-bubbles?
Czerlinski and Ypma: Yes, but details would have to be tested (micro-bubbles were specifically avoided in some experiments).
Reviewer: Information transfer between clusters is a vague notion, so how broad is the spectrum of wavelengths that mediates it?
Czerlinski and Ypma: At this point, we don’t really know, definitely from below 400 nm to at least 800 nm, but possibly up to km.
Reviewer: What is mesomery?
Czerlinski and Ypma: Mesomery = electronic isomery, see next answer.
Reviewer: How does mesomery stabilize your homeopathic agents (radicals)?
Czerlinski and Ypma: The electronic excitation level structure exists within a domain of (say) 20 water molecules, with one of these molecules replaced by either H. or OH. and the radical moving from one water molecule to the next by electronic rearrangement. In the copying process (in c3*) the electron distribution in the donor/original agent is transferred to the electron distribution in the acceptor/domain of water molecules; the electron in the domain then stays with each water molecule different lengths of times. For instance, if the donor is dipolar, the acceptor will also be dipolar. Intuitively, the original agent has a ‘hard’ electronic structure, when the water-domain has a ‘soft’ one. However, once the acceptor has a new electron probability distribution for at least 100 fs, the distances between individual water molecules in the domain will adjust, for which up to 100 ms (1/k3) is available. This should in turn affect electromagnetic absorption and emission spectra over a very wide range.
